Issues in loudspeaker design - 2

| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 | Page 6 | Page 7 |

M - Investigation of energy storage

N - Mounting a driver to a baffle

--------------------------------------------------------------------------------------------------------------------------------

M - Investigation of energy storage

Mechanical and electro-acoustic systems often have resonances and thus store energy, which is then gradually released. This is a linear phenomenon and in theory can always be corrected with equalizing filters. Thus, the Q of the electro-mechanical resonance, which determines the low frequency roll-off of a loudspeaker, is usually controlled or corrected during the design of the speaker. Equalization may become difficult or impractical in the high frequency region of a driver's operating range. If that is the case, then the severity of the resonance in terms of audibility must be assessed or a different driver must be found. Different tests and data presentations can be used to detect the presence of resonance. Here they will be applied to investigate a metal dome tweeter for usability in a speaker of high accuracy in sound reproduction.

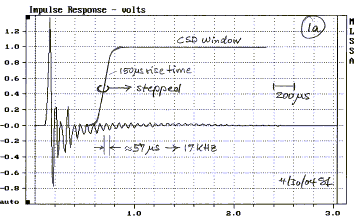
1 - The impulse response fully describes a linear system. The first 3 ms of the tweeter's impulse response (1) accurately describe its behavior above 330 Hz. The impulse response is made up of a large number of sinusoids (Fourier components). The longest full sinusoidal period that is contained in the time window is 3 ms long, corresponding to 330 Hz. Lower frequency content is progressively less well defined. The impulse response shows a dominant ringing with a frequency of around 17 kHz, which is indicative of a resonance.

Additional information can sometimes be gleaned from looking at the envelope of the impulse, as given by its energy-time curve (2). The ringing is shown to decay exponentially at a rate of 12.5 dB/ms. If it were caused by a single 2-pole resonator, then its 3 dB bandwidth would be 458 Hz and Q = 37. But what is really happening?

2 - Besides analyzing the impulse response, more information can usually be obtained from the graphical representation of its transform into the frequency domain. The magnitude response (3) clearly shows irregular behavior above 8 kHz, some of which is also noticeable in the phase response (4). How severe are the response deviations and can they be equalized readily? 

It is important to know how the data were taken. For the above measurements the microphone was at a distance of 0.5" (13 mm) from the "diffuser" in front of the metal dome. When the microphone is moved back, the shape of the response curve changes. Some details are lost, others are introduced. 

The driver was flush mounted on a 12" x 15" flat baffle. The impulse length was 25 ms for Figure (5). The loss in smoothness of the curves at greater distance is due to reflections from the baffle edge and other nearby objects. To minimize these a shorter impulse length could have been used, but that would have sacrificed low frequency accuracy which was desired for the following investigation. The microphone was at 0.5" from the tweeter.

3 -  A Fourier transform of the 25 ms impulse response, starting at time = 0,  yields the steady-state frequency response above 40 Hz. By multiplying the impulse response with a rectangular window that steps from left to right (1a), sequentially later sections of the response are transformed into the frequency domain. 

With the different frequency response slices  stacked along the time axis you obtain a cumulative spectral decay or waterfall presentation of the system response. In one graph you have both frequency and time information, but with some uncertainty and processing artifacts due to the necessary windowing of the impulse data.

The graph (6) begins with the steady-state response which persists for some time T₀ since the stepped window starts earlier in the data than the impulse response (1a). The progression of the frequency response slices with time is better seen from a different angle (7). Note the peculiar decay behavior below 1 kHz and especially below 100 Hz in (6) and (7). These are data processing artifacts. How high in frequency do they carry? The 1.2 ms block of decay response curves is barely longer than the 1 ms period of a 1 kHz sinewave. How much amplitude change can you even expect to see for the 1 kHz component during 1 ms? 

Around 6 kHz the waterfall drops at a maximum rate. This rate and the roundness of the amplitude versus time slice is a strong function of the stepped window rise time (1a). In this case the rise time was 0.15 ms for a half Blackman-Harris window. A faster rise time would give a steeper decay, but other artifacts may begin to show, depending upon the nature of the steady-state response. At 10 kHz and at 15.7 kHz resonant decay behavior can be clearly seen and with high frequency resolution. But, is it sufficiently quantifiable information to choose or reject this tweeter in comparison to another one?

4 - At each frequency the CSD response is related to the decay transient that occurs when a sinewave signal has reached steady-state response of the system and is then turned off suddenly. Because the spectrum of the turn-off step contains lower frequency components than the sinewave, it excites a system response to these frequencies, but the transient is falsely added to the display of the original sinewave turn-off response. For the same reason, rectangular envelope tone burst test signals produce misleading transient response data. When the envelope of the tone burst is shaped with a cosine contour or a Blackman window, then the system turn-on and turn-off becomes gradual and the response becomes indicative only to what is happening in the the frequency region under investigation. 

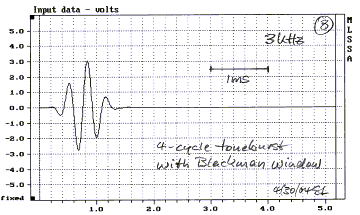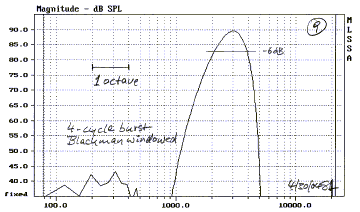
A 4-cycle shaped tone burst (8) is optimized towards fast rise and decay, while containing its spectral envelope (9) so that it still provides adequate frequency resolution. This signal operates in the "fuzzy" domain. Plotting the peak amplitude of the envelope gives a dynamic frequency response of the system, which can look different from the steady-state response. Observation of the decay of the burst response shows dynamic, time domain system behavior. Both amplitude and time tests using this test signal have shown strong correlation to subjective impressions. This type of signal has been the basis for a useful test system. Today, it should be part of sound card based computer test software. The response should be presented like a waterfall graph with a frequency and a number of cycles axis, rather than frequency and time axis like the CSD. 

For stored energy evaluation I compare the shape of the test signal to its response. The delay between the two is due to sound propagation and system delay. That in itself is of low importance in most cases compared to the decay response which shows the effects of energy storage. 

The 3 kHz response (10), for the tweeter above, is in the midst of its flat frequency response region (6). It shows good transient behavior. The response to all the frequencies indicated in (6) is given below.

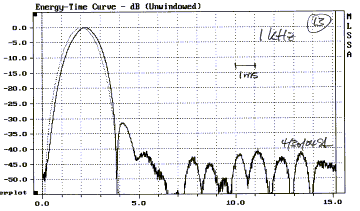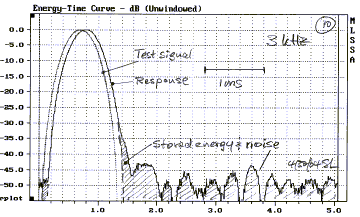
Note that all the burst responses below 3 kHz look as expected, unlike the CSD (7).

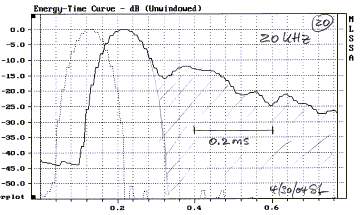
Clearly this driver has problems above 10 kHz. The cause for the resonance is the "diffuser" cap. It forms a  Helmholtz resonator by the compliance of the air trapped between cone and cap, and by the mass of a doughnut shaped ring of air around the circumference of the gap between cone and cap. Removing the cap causes severe roll-off in the high frequency response. Equalization of the modified driver might be a possibility. Whether it is worthwhile depends on the driver's non-linear performance, which requires different tests to determine.

The impulse, ETC, frequency, CSD and tone burst response give different representations of the same reality. Some are easier to interpret than others. Some are more related to certain aspects of linear distortion. There may be preferences depending upon one's experience with relating a visual feature to an auditory sensation. 

Further reading:
[1] Siegfried Linkwitz, "Shaped Tone-Burst Testing", JAES, Vol. 28, No. 4, April 1980, Abstract
[2] J. D. Bunton, R. H. Small, "Cumulative Spectra, Tone Bursts, and Apodization", JAES, Vol. 30, No. 6, pp. 386-395, June 1982
[3] O. Dossing, "Uncertainty in Time-Frequency Domain Representations", Sound and Vibration, Vol. 32, No. 1, January 1998, pp. 14-24
[4] Jochen Fabricius, "Eine alternative Methode zur Berechnung des kumulativen Zerfallspektrums". An alternative method for calculating a CSD. The system impulse response is convolved with shaped tone bursts. The derived waterfall presentation allows the visual separation of reflections from resonances. The conventional time axis is replaced by periods of the tone burst. (In German)
[5] Ivo Mateljahn, Heinrich Weber, Ante Doric, "Detection of Audible Resonances", 2007. From the Support page of the ARTA Audio Measurement and Analysis Software website.

Part 2 is a comparison between two high quality 8" drivers using CSD and burst tests.

N - Mounting a driver to a baffle

A cone type electro-dynamic driver is primarily a generator of mechanical vibration force and heat. It sets air into motion, but the reactive force of the air has insignificant influence on its behavior. For acoustic and mechanical reasons a driver is always mounted to a baffle of some form. Thus the forces generated in the driver try to set the baffle into motion. The resulting whole body movement is usually a small fraction of the cone movement and governed by the relative masses of cone and baffle. Mms v_cone = Mbaffle v_baffle. Since the cone velocity v_cone decreases with increasing frequency for constant SPL, the whole body motion is usually only noticeable at low frequencies and causes an insignificant reduction in SPL. This is a non-resonant phenomenon and no energy is stored. 

Take, for example, two woofer drivers where each has a cone of 135 g moving mass and both are mounted in a box of 60 lb total weight or 27 kg mass. The box will want to move in reaction to the cone movement by 270g / 27000g = 1 /100 of the cone. Thus a cone displacement of 10 mm leads to a box displacement of 0.1 mm in the opposite direction. You can feel this readily by lightly touching the box. The effective movement is 9.9 mm, and a reduction in acoustic output by 0.1 dB which is insignificant.

Fundamentally different from this is the excitation of panel vibration modes. These are always resonant, store energy and can radiate sound. Usually the baffle or box surface is larger than the cone area. Thus small modal displacements can lead to more sound being radiated directly from the baffle or box at certain frequencies than from the cone. Knocking with your knuckle on a panel can give you a rough idea of the dominant mode frequency, though it might not necessarily get excited by the driver. This test can also tell you how stiff the panel is, when the pitch is high, or how well the panel is damped because it hurts to make it respond. 

It is illustrative to look at the forces generated by a midrange driver at a given Sound Pressure Level.

The above excerpt from the spreadsheet SPL-dependent.xls is based on the textbook theory that was given in Publication (4). Note that at 90 dB SPL the 20 g moving mass, Mms, of the driver generates a g-force of 6.1 N or 1.4 lb rms between basket rim and magnet, a sinusoidal oscillating force of +/-2 lb peak. The cone undergoes a constant value acceleration of 30.9 g rms, or +/-43.6 g peak, at all frequencies. The peak cone excursion, Xpeak, is of course strongly frequency dependent and decreases as 1/f². The kinetic energy, 1/2 m v², falls off as 1/f². 
This same driver mounted on an open baffle and equalized to remove the 6 dB/oct dipole cancellation will have larger excursions below Fequal than when in a closed box. Therefore the forces are larger and frequency dependent. Likewise the kinetic energy is higher, but falling off as 1/f³.
The spreadsheet also shows the large force and extreme acceleration experienced by a tweeter dome, though the kinetic energy is quite small due to a low moving mass.

There are several ways to reduce modal panel vibrations. Because the vibration energy from the driver decreases rapidly with increasing frequency it is advantageous to push the panel vibration modes up in frequency where the excitation energy is small. This is best accomplished by increasing the panel stiffness, but often goes together with increasing the mechanical Q of resonance. Dampening the panel by using a constrained layer that dissipates energy will reduce Q. Panel stiffness is also obtained by extensive bracing. As my rule of thumb, no un-braced box panel area should be larger than 4 inch squared for 3/4 inch thick wood panels. That is a lot of bracing, but it pushes modes into the low kHz range. 

Increasing the thickness of a panel makes good sense when the resulting increase in stiffness is larger than the increase in mass. Otherwise modal resonance could occur lower in frequency than for the thin panel. Still, the increase in mass requires larger amounts of excitation energy and can therefore be beneficial.
Panel vibration modes are not only excited by structure borne vibration energy but also by air borne vibration such as the large sound pressure inside a box loudspeaker. Even if the box panels are infinitely stiff, secondary delayed sound will leak out through the thin cone material at higher frequencies where air modes can exist inside the box. A perfect acoustic resistor to absorb all sound is not available.

There is yet another potential problem with the driver to baffle interface, even if the baffle is perfectly inert. It is related to the mechanical construction of the driver itself and how it can become a mechanical resonator of its own. 
Typically a loudspeaker driver has screw holes in its basket for mounting it to a baffle. Usually a sealing gasket is placed between the driver basket rim and the baffle. The driver becomes in effect stiffly clamped to the baffle. This method sets up a mechanically resonant structure which is formed by the compliance of the basket and the mass of the magnet as seen in figure (A).

A)  Drivers with a stamped metal baskets are prone to exhibit a high Q resonance when tightly clamped to the baffle. The magnet moves relative to the voice coil at the resonance frequency. Energy is stored and also readily transmitted from the moving mass of the cone into the cabinet. B) Soft mounting the driver basket to the baffle using rubber grommets reduces the resonance frequency. A 2nd order lowpass filter is formed that reduces the transmission of vibration energy from the moving cone to the baffle and cabinet. The resonance must occur below the operating range of the driver. C) If the driver is mounted from the magnet and the basket rim touches the baffle only softly, then the magnet-basket resonance cannot occur and the transmission of vibration energy into the baffle is minimized.

The basket-magnet resonance can be measured with an accelerometer that is mounted to the magnet. The drive signal is optimally a shaped toneburst. Its energy is concentrated in a narrow frequency band. When tuned to the right frequency a long decay tail becomes visible on an oscilloscope. Often the resonance can be seen as a small bump in the driver's impedance curve in the few hundred Hz range. It should not be confused with the higher frequency bump due to cone breakup. 

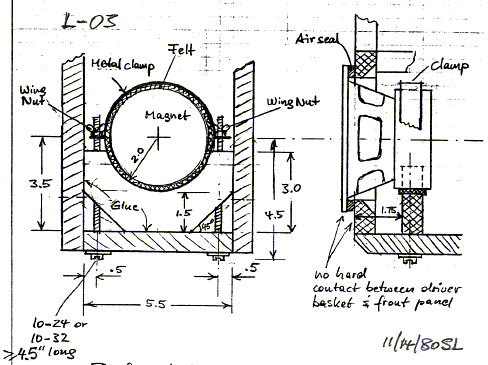An early example of a box loudspeaker where a KEF B110 midrange/woofer driver magnet is clamped to a support structure. The clamp can be tightened from the outside of the box. The basket rim is floating.

Often the effects due to driver mounting are deemed to be of secondary importance to the overall sound quality of a loudspeaker. They are usually costly to remedy. They cannot be ignored when the goal is to design a loudspeaker of the highest accuracy.

| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 | Page 6 | Page 7 |